树状数组(二叉索引树)--Binary_Indexed_Tree

树状数组

简介

树状数组或二叉索引树(Binary Indexed Tree, BIT)，又以其发明者命名为Fenwick Tree。可以解决大部分区间上面的修改以及查询的问题，例如1.单点修改，单点查询；2.区间修改，单点查询；3.区间查询，区间修改。

树状数组的结构

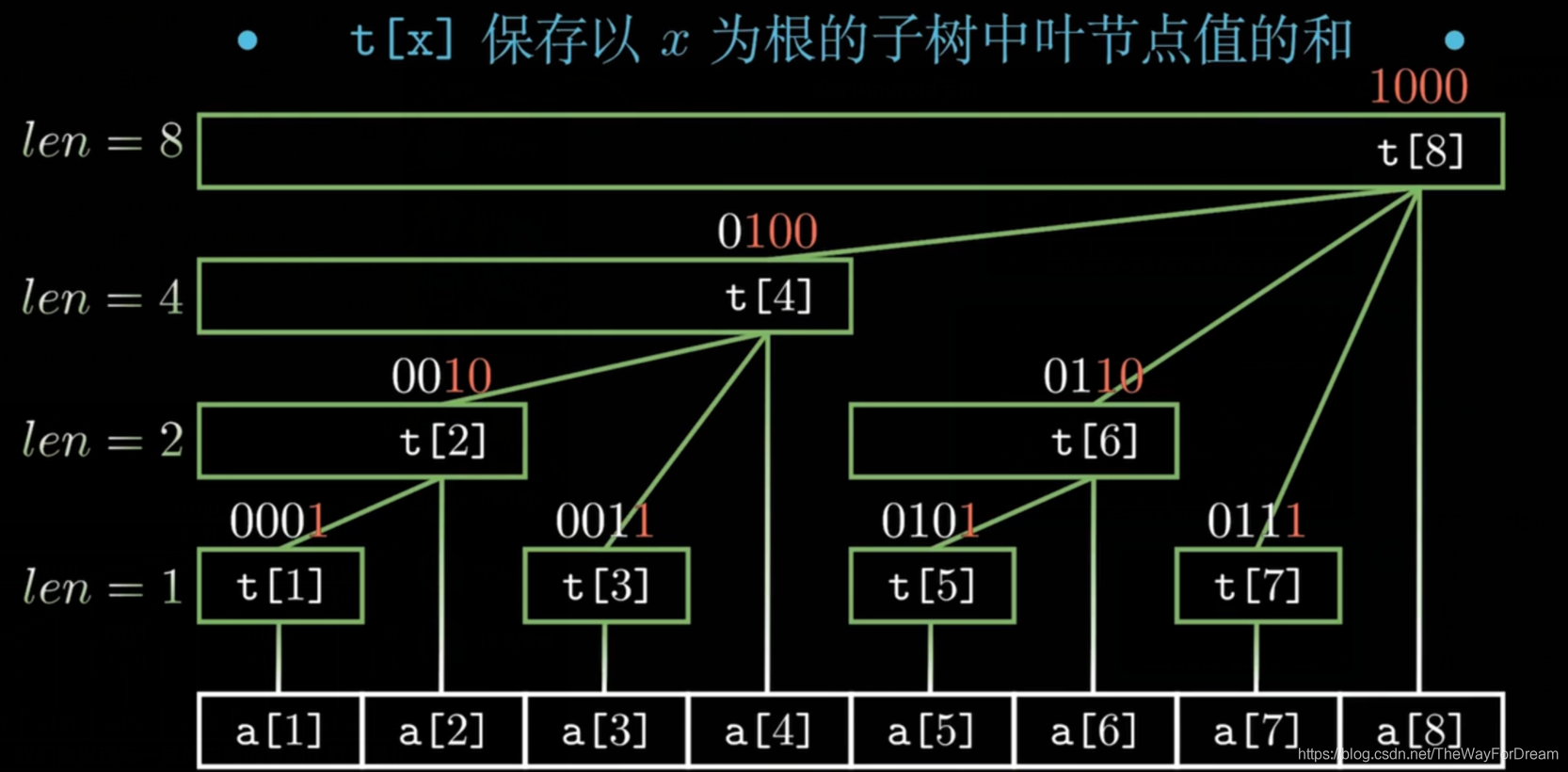
$lowbit(x)$运算

如何计算一个非负整数n在二进制下的最低为1及其后面的0构成的数？例如：$44 = (101100)_2$，最低位的1和后面的0构成的数是$(100)_2 = 4$，所以$lowbit(44) = lowbit((101100)_2) = (100)_2 = 4$

$lowbit(x)$运算的实现通过原数与取反数的按位与得到，即：$lowbit(x)=x\&(-x)$，其中，$-x$以$x$的补码形式表示。

树状数组的相关操作

• 单点修改，区间查询

单点修改：迭代更新x，即每次更新其父节点，令$x=x+lowbit(x)$，再将父节点的值加$k$。

int add_dandian(int x, int k){
	for(int i = x; i <= n;i += lowbit(i))
	t[i] += k;
}

区间查询：迭代更新x，令$x=x-lowbit(x)$，再将此节点的值加到求和的变量中。

int ask(int x){
	int sum = 0;
	for(int i = x; i >= 1; i -= lowbit(i)){
		sum += t[i];
	}
	return sum;
}

• 区间修改，单点查询

对于这一类操作，我们需要构造出原数组的差分数组$b$，然后用树状数组维护$b$数组即可。

对于区间修改，只需要对差分数组进行操作即可，例如对区间$[L,R]+k$,那么我们只需要更新差分数组$add(L,k)$，$add(R+1,-k)$，这是差分数组的性质。

int update(int pos, int k){  //pos表示修改点的位置,K表示修改的值也即+K操作
	for(int i = pos; i <= n; i += lowbit(i)) c[i] += k;
	return 0;
}
update(L, k);
update(R+1, -k);

对于单点查询操作，求出b数组的前缀和即可，因为$a[x]=$差分数组$b[1]+b[2]+…+b[x]$的前缀和，这是差分数组的性质之一。

ll ask(int pos){
	ll ans = 0;
	for(int i = pos; i >= 1; i -= lowbit(i)) ans += c[i];
	return ans;
}