AcWing_4646 爬树的甲壳虫(同余意义下的逆元、费马小定理、快速幂、递推公式)

AcWing

4646. 爬树的甲壳虫(第十三届蓝桥杯省赛C++ A组/C组)

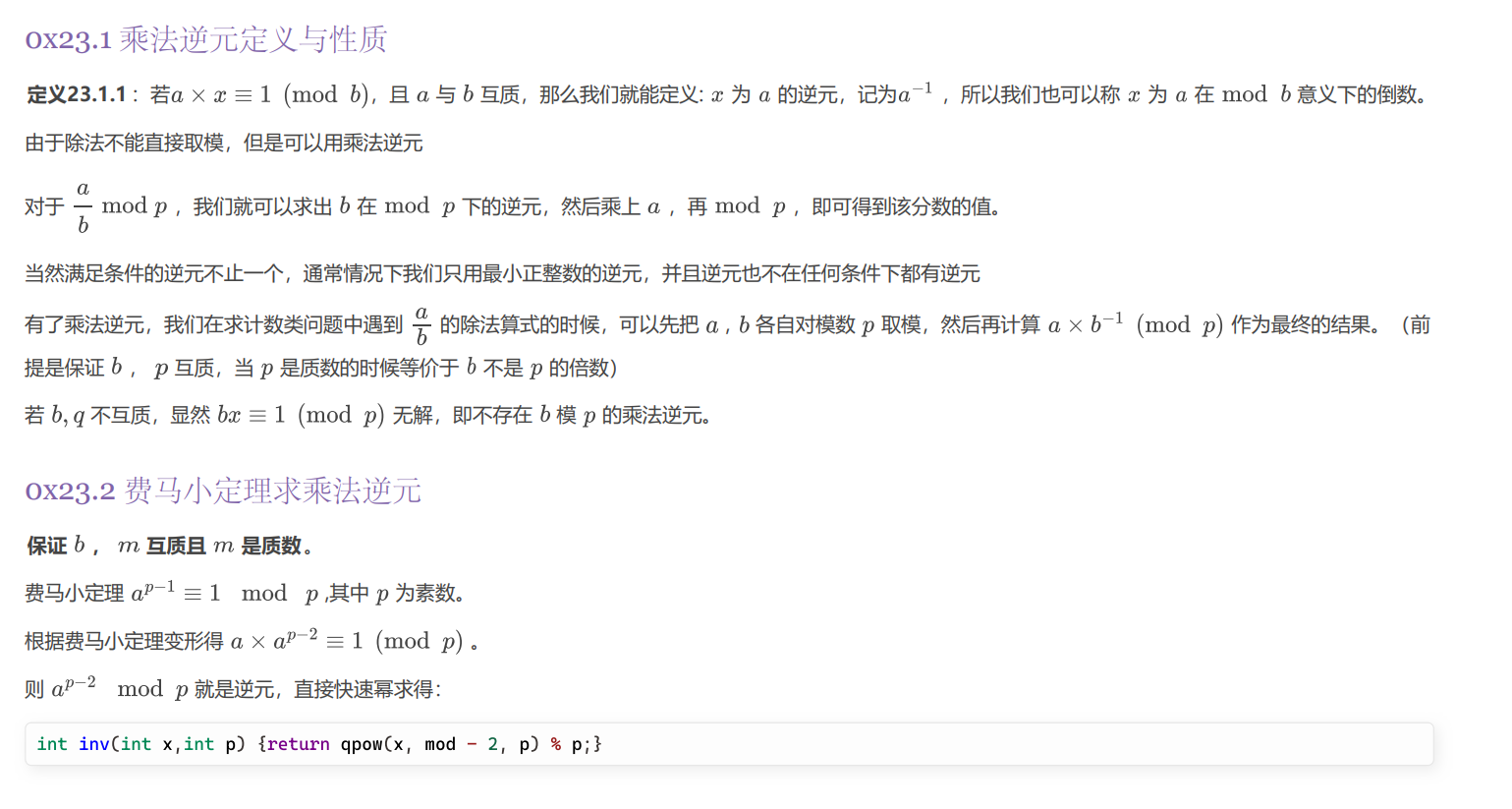
(费马小定理除了要求$p$是质数，还要求$b$不被$p$整除，即$b$不是$p$的倍数)

$\frac{a}{b}\equiv ax\mod p$，其中$b$、$p$互质，那么称$x$是$b$的模$p$乘法逆元，它将难以求余数的分数(有理数)转化为便于求余数的乘法整数值。

$x$是$b$的模$p$乘法逆元，那么有$bx\equiv 1\mod p$.

根据费马小定理，当$p$是质数，且$b$不被$p$整除(即$b$不是$p$的倍数)，那么$b^{p-1}\equiv 1\mod p$，即$b*b^{p-2}\equiv 1\mod p$，那么：

$b^{p-2}$就是$b$的模$p$乘法逆元(也可写作$inv(b)=b^{p−2}\mod p$)；

特殊地，如果$b$被$p$整除，那么$b$的模$p$乘法逆元不存在，因为$b\equiv 0\mod p$，恒有$b*x\equiv 0\mod p$，不可能有$b^{p-1}\equiv 1\mod p$.

板子：

int qmi(int a, int k, int p){
    int res = 1 % p;
    while(k){
        if(k & 1) res = (LL)res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}
int inv(int a, int p){  // a的模p逆元
    return qmi(a, p - 2, p);
}

公式的推导：

令f[i]：从0到i的期望时间，那么，如果要爬到树i高度的位置：

$f[i] = f[i-1] + (1-p_i) * 1 + p_i * (1+f[i])$

其中，f[i-1]表示先到树i-1高度的位置，所需要的期望时间，之后，如果成功爬上一层，花费的时间是1，否则，不仅当前尝试爬的时间1要浪费，还要再花费f[i]的期望时间，来爬到树i高度的位置。

展开，化简，代入$p_i = \frac{x_i}{y_i}$，得到：

$f[i] = \frac{y_i(f[i-1] + 1)}{y_i-x_i}$

求f[i] % MOD，先求y(f[i-1]+1) % MOD，再求y-x的逆元inv(y-x)，最后求y(f[i-1]+1) % MOD * inv(y-x) % MOD.

遍历的时间复杂度是$O(n)$，快速幂的时间复杂度是$O(logn)$，所以总的时间复杂度是$O(nlogn)$.

代码：

#include <bits/stdc++.h>
using namespace std;
int n, f = 0;
const int MOD = 998244353;
typedef long long LL;
int qmi(int a, int k, int p){
    int res = 1 % p;
    while(k){
        if(k & 1) res = (LL)res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}
int inv(int a, int p){
    return qmi(a, p - 2, p);
}
int main(){
    cin >> n;
    while(n--){
        int x, y;
        cin >> x >> y;
        f = ((LL)f + 1) * y % MOD * inv((y - x), MOD) % MOD;
    }
    cout << f << endl;
    return 0;
}