AcWing
876. 快速幂求逆元
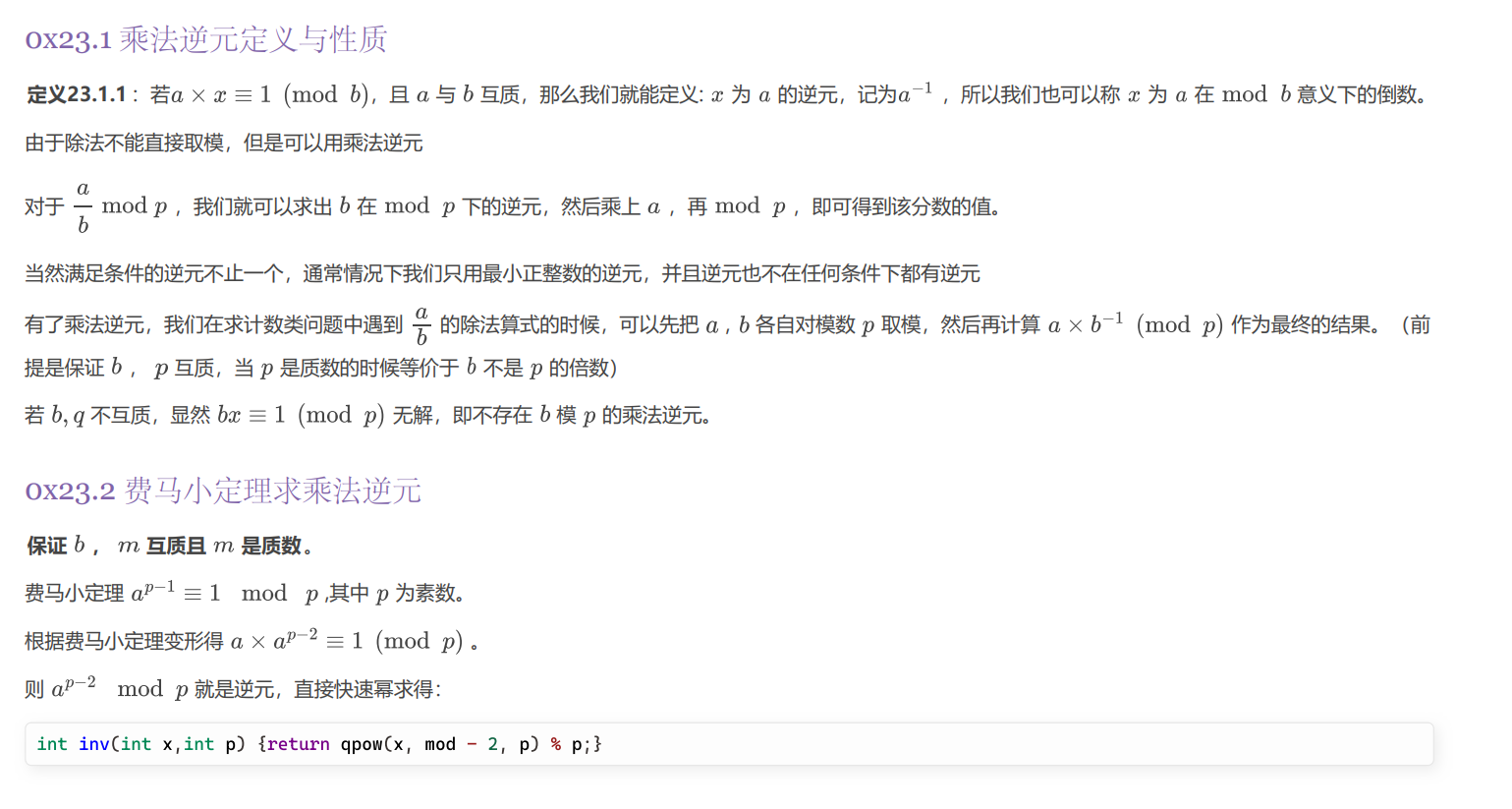
(费马小定理除了要求$p$是质数,还要求$b$不被$p$整除,即$b$不是$p$的倍数)
$\frac{a}{b}\equiv ax\mod p$,其中$b$、$p$互质,那么称$x$是$b$的模$p$乘法逆元,它将难以求余数的分数(有理数)转化为便于求余数的乘法整数值。
$x$是$b$的模$p$乘法逆元,那么有$bx\equiv 1\mod p$.
根据费马小定理,当$p$是质数,且$b$不被$p$整除(即$b$不是$p$的倍数),那么$b^{p-1}\equiv 1\mod p$,即$b*b^{p-2}\equiv 1\mod p$,那么:
$b^{p-2}$就是$b$的模$p$乘法逆元(也可写作$inv(b)=b^{p−2}\mod p$);
特殊地,如果$b$被$p$整除,那么$b$的模$p$乘法逆元不存在,因为$b\equiv 0\mod p$,恒有$b*x\equiv 0\mod p$,不可能有$b^{p-1}\equiv 1\mod p$.
板子:
int qmi(int a, int k, int p){
int res = 1 % p;
while(k){
if(k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
return res;
}
int inv(int a, int p){ // a的模p逆元
return qmi(a, p - 2, p);
}
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
typedef long long LL;
int qmi(int a, int k, int p){
int res = 1 % p;
while(k){
if(k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
return res;
}
int main(){
cin >> n;
while(n--){
int a, p;
cin >> a >> p;
int res = qmi(a, p - 2, p);
if(a % p) cout << res << endl;
else cout << "impossible" << endl;
}
return 0;
}
