线段树
简介
线段树可以解决大部分区间上面的修改以及查询的问题:单点修改、单点查询、区间修改、区间查询。
参考: 线段树:从没入门到入门
线段树的结构
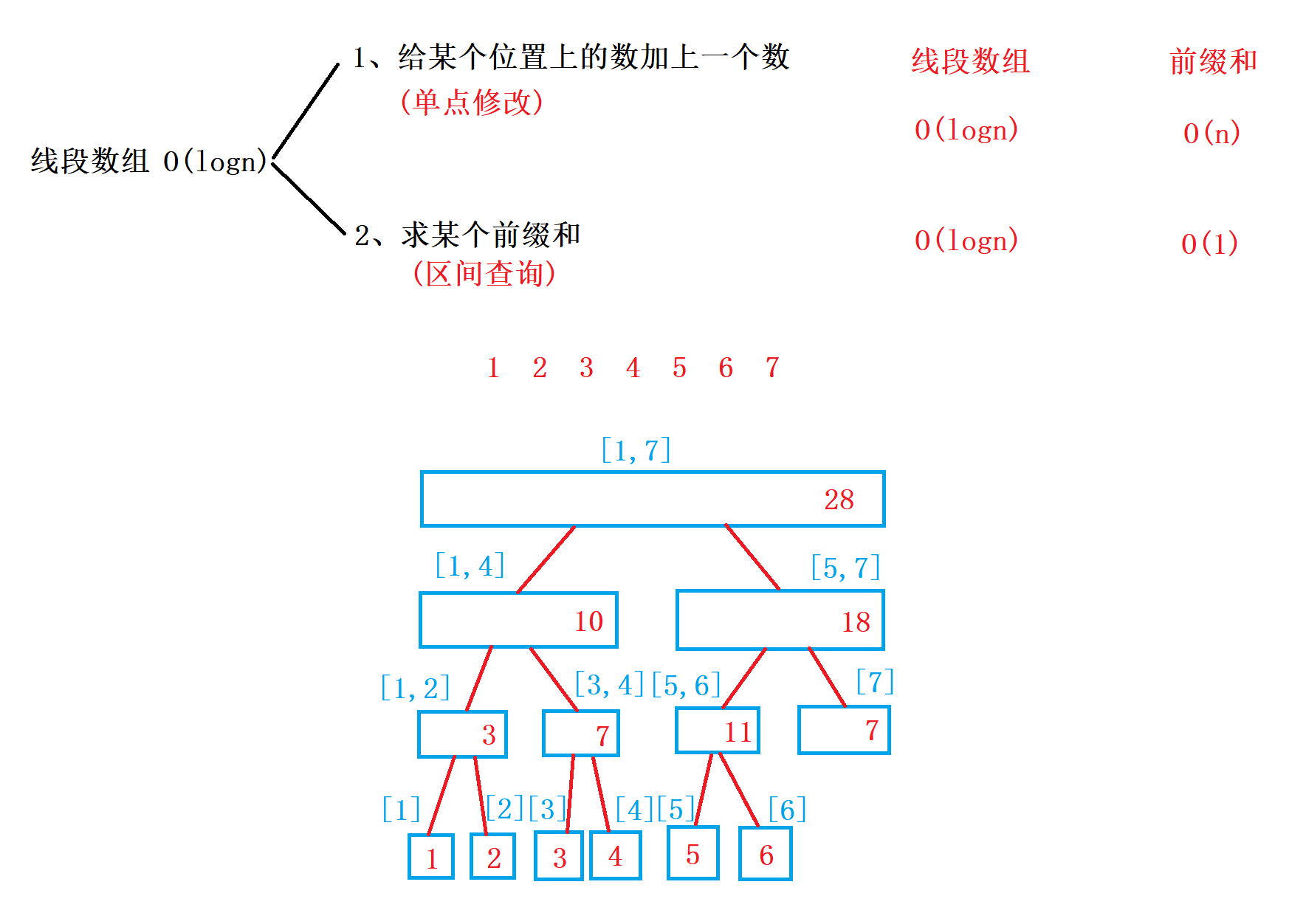
构造(从1开始编号)
int a[n]; // 原数组
int sum[n*4]; // 开四倍n的大小
void push(int u){ // 由左右儿子更新父节点
sum[u] = sum[u*2] + sum[u*2 + 1];
}
void build(int l, int r, int u){ // (子)树的左边界、右边界、根节点
if(l == r) sum[u] = a[l];
else{
int mid = (l + r) / 2;
build(l, mid, u*2); // 递归建立左子树
build(mid + 1, r, u*2 + 1); // 递归建立右子树
push(u); // 更新子树根节点的值
}
}
线段树的相关操作
- 单点修改
void update(int a, int l, int r, int u, int v){ //要修改的点、子树的左边界、子树的右边界、子树的根节点,要增加的值
if(l == r){
a[u] += v; //修改点(原数组)
sum[u] += v; //修改和
}
else{ // 折半查找
int mid = (l + r) / 2;
if(a <= mid) update(a, l, mid, u*2, v); //递归查找左子树
else update(a, mid + 1, r, u*2 + 1, v); //递归查找右子树
push(u); // 更新子树根节点的值
}
}
- 区间修改
void down(int l, int r, int u){ // 下传lazy标记
if(tag[u]){ // 如果该节点有lazy标记
int mid = (l + r) / 2;
tag[u*2] += tag[u]; //下传给左子树
tag[u*2 + 1] += tag[u]; //下传给右子树
sum[u*2] += tag[u] * (mid - l + 1); //修改左子树和,因为该节点下面有(mid-l+1)个节点,每个节点+tag[u]
sum[u*2 + 1] += tag[u] * (r - mid); //修改右子树和,因为该节点下面有(r-mid)个节点,每个节点+tag[u]
tag[u] = 0; //该节点的lazy标记已传给左右儿子节点
}
}
void update(int L, int R, int l, int r, int u, int v){ //修改区间的左端点、右端点,线段树的左边界、右边界,子树的根节点,要加的值
if(l >= L && r <= R){ // 当修改区间完全覆盖当前子树的区间,把当前子树的区间和修改,并修改该节点的lazy标记值
tag[u] += v;//修改点
sum[u] += v * (r - l + 1); //修改和,因为该节点下面有(r-l+1)个节点,每个节点+v
}
else{
down(l, r, u); // 下传lazy标记
int mid = (l + r) / 2;
if(L <= mid) update(L, R, l, mid, u*2, v); // 递归修改左子树
if(mid < R) update(L, R, mid + 1, r, u*2 + 1, v); // 递归修改右子树
push(o); // 更新子树根节点的值
}
}
- 单点查询
int tag[n*4], sum[n*4], ans;
void down(int l, int r, int u){ // 下传lazy标记
if(tag[u]){ // 如果该节点有lazy标记
int mid = (l + r) / 2;
tag[u*2] += tag[u]; //下传给左子树
tag[u*2 + 1] += tag[u]; //下传给右子树
sum[u*2] += tag[u] * (mid - l + 1); //修改左子树和,因为该节点下面有(mid-l+1)个节点,每个节点+tag[u]
sum[u*2 + 1] += tag[u] * (r - mid); //修改右子树和,因为该节点下面有(r-mid)个节点,每个节点+tag[u]
tag[u] = 0; //该节点的lazy标记已传给左右儿子节点
}
}
void query(int l,int r,int u,int a){ //线段树左边界,右边界,节点(从1开始),查找位置
if(l == r) ans = sum[u]; // 查找到
else{ // 折半查找
down(l, r, u); // 下传lazy标记,修改子节点,再往子节点找
int mid = (l + r) / 2;
if(a <= mid) query(l, mid, u*2, a); // 查找左子树
else query(mid + 1, r, u*2 + 1, a); // 查找右子树
}
}
- 区间查询
int tag[n*4], sum[n*4];
void down(int l, int r, int u){ // 下传lazy标记
if(tag[u]){ // 如果该节点有lazy标记
int mid = (l + r) / 2;
tag[u*2] += tag[u]; //下传给左子树
tag[u*2 + 1] += tag[u]; //下传给右子树
sum[u*2] += tag[u] * (mid - l + 1); //修改左子树和,因为该节点下面有(mid-l+1)个节点,每个节点+tag[u]
sum[u*2 + 1] += tag[u] * (r - mid); //修改右子树和,因为该节点下面有(r-mid)个节点,每个节点+tag[u]
tag[u] = 0; //该节点的lazy标记已传给左右儿子节点
}
}
int query(int L, int R, int l, int r, int u){ //查询区间左端点、右端点,子树左边界,右边界,子树根节点
int ans = 0;
if(l >= L && r <= R) return sum[u]; // 当查询区间完全覆盖当前子树的区间,返回子树的值
else{
down(l, r, u); // 当查询区间不完全覆盖当前子树的区间,则下传lazy标记,修改子区间的和,然后再往子区间找
int mid=(l + r) / 2;
if(mid >= L) ans += query(L, R, l, mid, u*2);
if(mid < R) ans += query(L, R, mid + 1, r, u*2 + 1);
return ans;
}
}
