AcWing
1228. 油漆面积
扫描线套路:
从每个矩形的竖边,都做一条垂直的线,画完竖线之后统计面积。统计面积的方法:以每个柱形区域为单位来统计,如下图,每个颜色代表一个柱形区域。
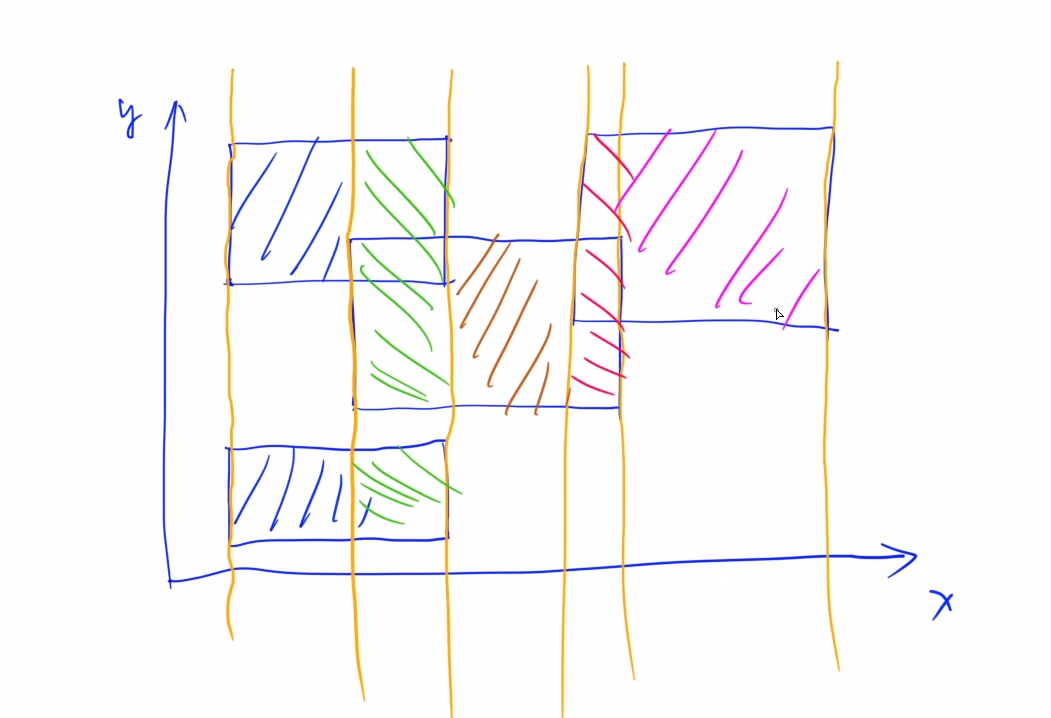
每个柱形区域的面积就是这个长条的宽度×阴影部分覆盖的高度
现在的问题就变成了:如何快速统计出来每个区间内部阴影部分的高度。这就需要用到一种非常特殊的线段树,之所以称之为“非常特殊”是因为这个做法比较难扩展,只适用于这一类题型。
定义sum[4*N]:覆盖度不小于1的区间长度,即线段树的维护值;
定义tag[4*N]:lazy标记,表示每个纵坐标区间当前的覆盖度
扫描线题型会用到lazy标记延迟更新的思想,这类题型特殊的地方就是它的lazy标记不下传,这是因为题目中对tag的增减操作成对出现,并且题目所求的结果只需要访问根节点的sum值,即整个纵坐标区间被覆盖的长度,只需要这个值在当前是实际正确的即可。即使在区间修改时不下传标记,修改儿子节点后的回溯值实际会被tag覆盖掉(因为优先判断tag是否存在),当tag移除时,当前节点的sum会重新计算。
操作步骤:
- 首先把每个矩形的左右两个边拿出来,变成一个三元组。(线段树维护的是纵坐标,把每个矩形的竖边看成一个带权值的线段);
- 第一个操作是给区间
[y1,y2]更新+1,表示这个矩形已经过来了(想象一下,竖线是扫描线,固定不动,一个个矩形从右向左飘过来); - 第二个操作是给区间
[y1,y2]更新-1,表示这个矩形已经全部穿过扫描线离开了。
再详细一点,我们规定,每个矩形的左竖边权值为+1,右竖边权值为-1,每次经过扫描线时,扫描线上的tag会加上或减去经过它的矩形的竖边的权值,所以在算每两个竖线之间阴影部分面积时,阴影部分的高度就是扫描线上此时的sum,也就是根结点的sum.
小细节:线段树在本题中维护的是一系列区间(用左端点代表),而不是一系列点值,所以坐标y1~y2的范围,相当于线段树中索引从y1到y2-1.
#include <bits/stdc++.h>
using namespace std;
int n;
const int N = 10010;
struct segment{
int x, y1, y2; // 仅考虑所有竖向的线段,线段的x坐标,起始y坐标,终止y坐标
int k; // 线段是矩形的左边还是右边,1 / -1
bool operator < (const segment &t) const{ // 按x坐标从小到大将所有线段排序
return x < t.x;
}
}segs[N*2];
int sum[4*N]; // 覆盖度不小于1的区间长度,即线段树的维护值
int tag[4*N]; // 涉及区间修改,使用lazy标记,表示每个纵坐标区间当前的覆盖度
void push(int l, int r, int u){
if(tag[u]) sum[u] = r - l + 1;
else if(l == r) sum[u] = 0; // 根节点,且没有标记
else sum[u] = sum[2*u] + sum[2*u + 1];
}
void update(int L, int R, int l, int r, int u, int v){
if(L <= l && r <= R){
tag[u] += v;
push(l, r, u);
}
else{
int mid = l + r >> 1;
if(L <= mid) update(L, R, l, mid, 2*u, v);
if(R > mid) update(L, R, mid + 1, r, 2*u + 1, v);
push(l, r, u);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
segs[i].x = x1, segs[i].y1 = y1, segs[i].y2 = y2, segs[i].k = 1;
segs[n + i].x = x2, segs[n + i].y1 = y1, segs[n + i].y2 = y2, segs[n + i].k = -1;
}
sort(segs + 1, segs + 1 + 2*n);
int res = 0;
for(int i = 1; i <= 2*n; i++){
if(i > 1) res += (segs[i].x - segs[i - 1].x) * sum[1];
update(segs[i].y1, segs[i].y2 - 1, 0, 10000, 1, segs[i].k);
}
cout << res;
return 0;
}
