AcWing
112. 雷达设备
(贪心) $O(nlogn)$
如下图所示,对于任意一个小岛$(x,y)$,我们都可以在海岸线上求出能覆盖该小岛的建造雷达的区间$[a,b]$.
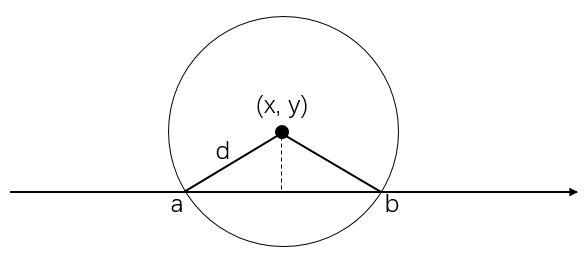
由勾股定理可知:
$a=x-\sqrt{d^2-y^2}$,
$b=x+\sqrt{d^2-y^2}$.
将所有小岛转化成区间后,问题转化为:给定$n$个区间,在$x$轴上选择尽量少的点,使得所有区间至少包含一个点。
算法步骤:
- 将所有区间按右端点从小到大排序;
- 依次考虑每个区间:
- 如果当前区间包含最后一个选择的点,则直接跳过;
- 如果当前区间不包含最后一个选择的点,则在当前区间的右端点的位置选一个新的点。
#include <bits/stdc++.h>
using namespace std;
int n, d;
const int N = 1010;
typedef pair<double, double> PDD;
#define xx first
#define yy second
PDD seg[N];
const double eps = 1e-6;
bool cmp(PDD u, PDD v){ return u.yy < v.yy; }
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> d;
for(int i = 0; i <= n - 1; i ++){
int x, y;
cin >> x >> y;
if(y > d){
cout << -1;
return 0;
}
seg[i].xx = x - sqrt(d * d - y * y);
seg[i].yy = x + sqrt(d * d - y * y);
}
sort(seg, seg + n, cmp);
int res = 0;
double rr = seg[0].xx - 1;
for(int i = 0; i <= n - 1; i ++){
if(seg[i].xx <= rr) continue;
rr = seg[i].yy;
res ++;
}
cout << res;
return 0;
}
