本篇部分参考自https://blog.csdn.net/AugustMe/article/details/109673270
目录
- 目录
- 最大池化(Max Pooling)
- 平均池化(Average Pooling)
- 随机池化(Stochastic Pooling, ICLR 2013)
- 全局平均池化(Global Average Pooling, NIN 2013)
- 空间金字塔池化(Spatial Pyramid Pooling, TPAMI 2015)
- 双线性池化(Bilinear Pooling, ICCV 2015)
最大池化(Max Pooling)
最大池化是对邻域内特征点取最大。优点是能很好地保留图像的纹理特征。一般常用MaxPooling,而少用AvgPooling,因为通常来说,MaxPooling的效果更好,虽然MaxPooling和AvgPooling都对数据做了下采样,但是MaxPooling感觉更像是做了特征选择,选出了分类辨识度更好的特征,提供了非线性。
正向传播:取邻域内最大,并记住最大值的索引位置,以方便反向传播。
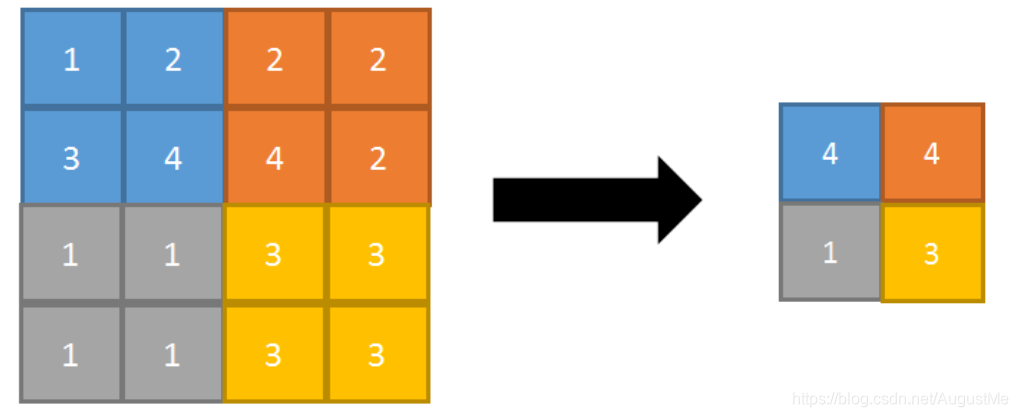
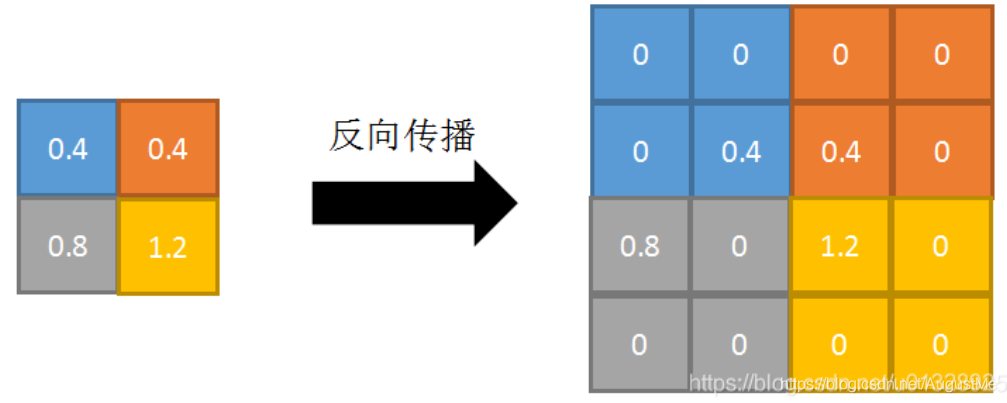
反向传播:将特征值填充到正向传播中值最大的索引位置,其他位置补0。
平均池化(Average Pooling)
平均池化是对邻域内特征点求平均。优点是能很好地保留图像的背景信息。AvgPooling更强调对整体特征信息进行一层下采样,在减少参数维度的贡献上更大一点,更多地体现在信息的完整传递这个维度上,在一个很大很有代表性的模型中,比如说DenseNet中的模块之间的连接,大多采用了AvgPooling,在减少维度的同时,更有利于信息传递到下一个模块进行特征提取。
正向传播:取邻域内平均。
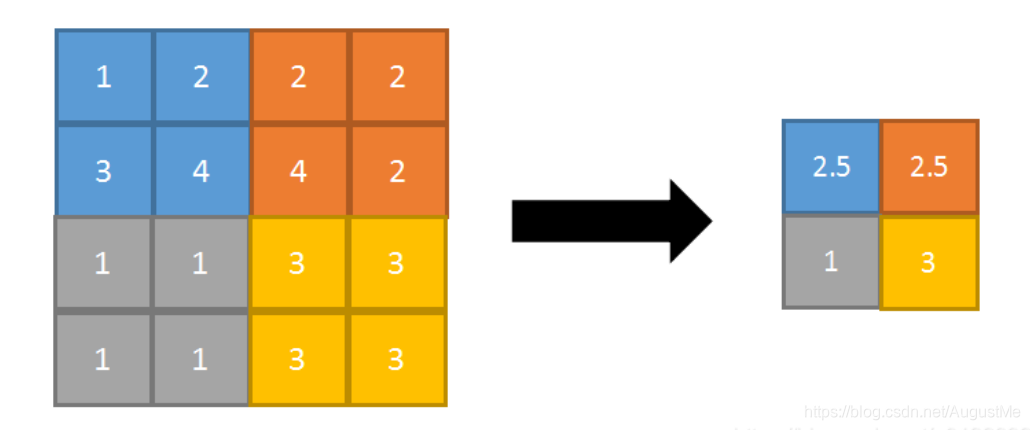
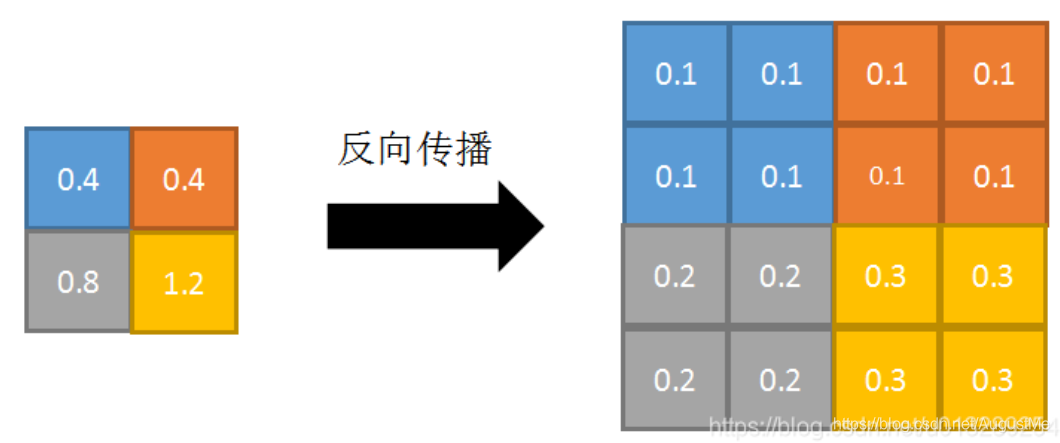
反向传播:特征值根据邻域大小被平均,然后传给每个索引位置。
随机池化(Stochastic Pooling, ICLR 2013)
随机池化对特征图中的元素按照其概率值大小随机选择,即元素值大的被选中的概率也大。而不像Max Pooling那样,永远只取那个最大值元素。相比之下,它的优点在于泛化能力更强(带有随机性)。
在区域内,将数值进行归一化处理,即$1/(1+2+3+4)=0.1$;$2/10=0.2$;$3/10=0.3$;$4/10=0.4$。

接着按照概率值来随机选择,一般情况下,概率大的更容易被选择到。例如,选择到了概率值为0.3的时候,那么(1, 2, 3, 4)池化之后的值为3。使用Stochastic Pooling时,其推理过程(即test过程)也很简单,对矩阵区域求加权平均即可,比如上图中,池化输出值为:$1 \times 0.1 + 2 \times 0.2 + 3 \times 0.3 + 4 \times 0.4 = 3$(期望值)。在反向传播求导时(train过程),只需保留前向传播已经记录被选中节点的位置的值,其它值都为0,这和Max Pooling的反向传播非常类似。
全局平均池化(Global Average Pooling, NIN 2013)
全局平均池化一般是用来替换全连接层。在分类网络中,全连接层几乎成了标配,在最后几层,特征图会被reshape成向量,接着对这个向量做乘法,最终降低其维度,然后输入到softmax层中得到对应的每个类别的得分。过多的全连接层,不仅会使得网络参数变多,也会产生过拟合现象。针对过拟合现象,全连接层一般会搭配dropout操作。而全局平均池化则直接把整个特征图(的每个通道,特征图通道数等于类别数)进行平均池化,然后输入到softmax层中得到对应的每个类别的得分。在反向传播求导时,它的参数更新和平均池化很类似。
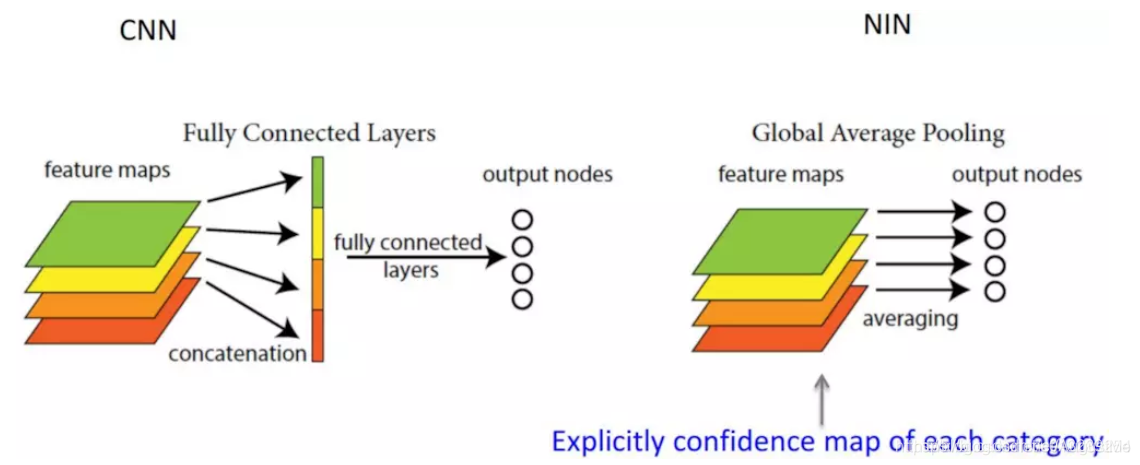
它的优点是大幅度减少网络参数(对于分类网络,全连接的参数占了很大比例),同时理所当然地减少了过拟合。赋予了输出特征图的每个通道类别意义,剔除了全连接黑箱操作。
空间金字塔池化(Spatial Pyramid Pooling, TPAMI 2015)
在现有的CNN中,对于结构已经确定的网络,需要输入一张固定大小的图片。这样,在希望检测各种大小的图片的时候,需要经过裁剪或者缩放等一系列操作,这样往往会降低识别检测的精度。空间金字塔池化(SPP)使得构建的网络可以输入任意大小的图片,不需要经过裁剪缩放等操作,检测精度也会有所提高。
下图的上部分是传统的CNN结构,下部分是应用了SPP池化CNN结构。这个卷积层可以接受任意大小的输入,但是经过SPP之后会产生固定大小的输出以适应全连接层,大小由SPP结构而定。

SPP的具体结构如下图所示:
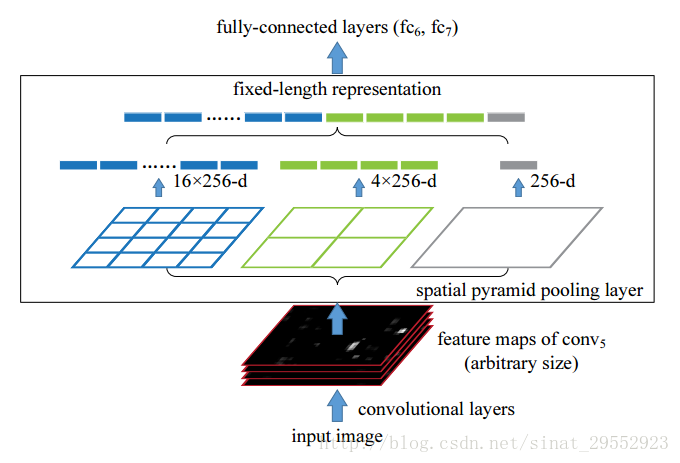
把前一卷积层的特征图的每一个通道(假设有256个通道)上进行了3种池化操作。最右边是对特征图的每一个通道做全局池化(论文中给出的是MaxPooling);中间的是把特征图的每一个通道分成4份,对每一份全局池化;最左边是把特征图的每一个通道分成16份,对每一份全局池化。之后再拼接池化的结果。这就解决了特征图大小不一的状况了。
但是SPP也存在一定的缺点,就是BP训练困难。在Fast R-CNN中写道:The root cause is that back-propagation through the SPP layer ishighly inefficient when each training sample (i.e. RoI) comes from a different image。
双线性池化(Bilinear Pooling, ICCV 2015)
用于Fine-Grained分类,主要用于特征融合,对于从同一个样本中提取到的特征$x$和$y$,通过Bilinear Pooling得到两个特征融合后的向量,进而用于分类。
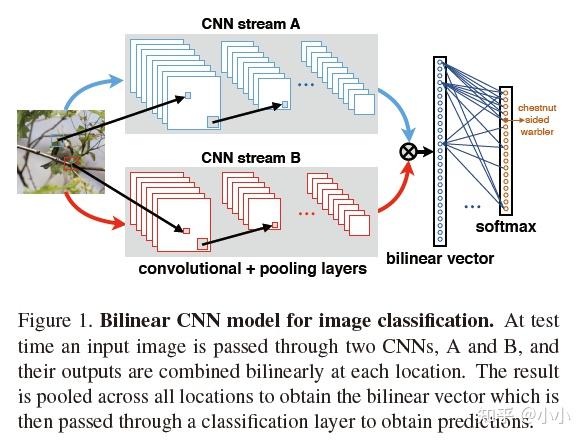
- Multimodel Bilinear Pooling,如果特征$x$和$y$分别来自两个特征提取器,则称为多模双线性池化;
- Homogeneous Bilinear Pooling,如果特征$x$和$y$分别来同一个特征提取器,则称为同源双线性池化。
